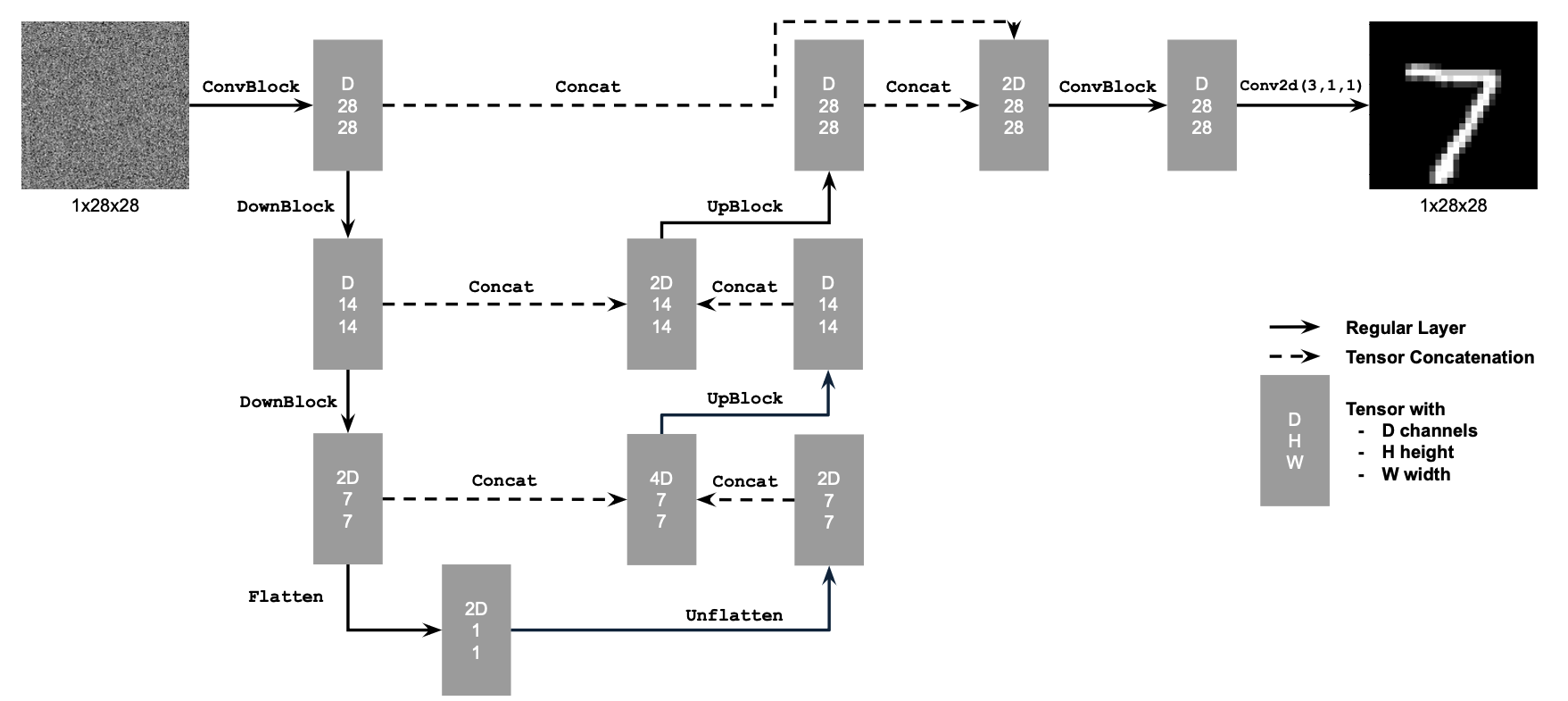
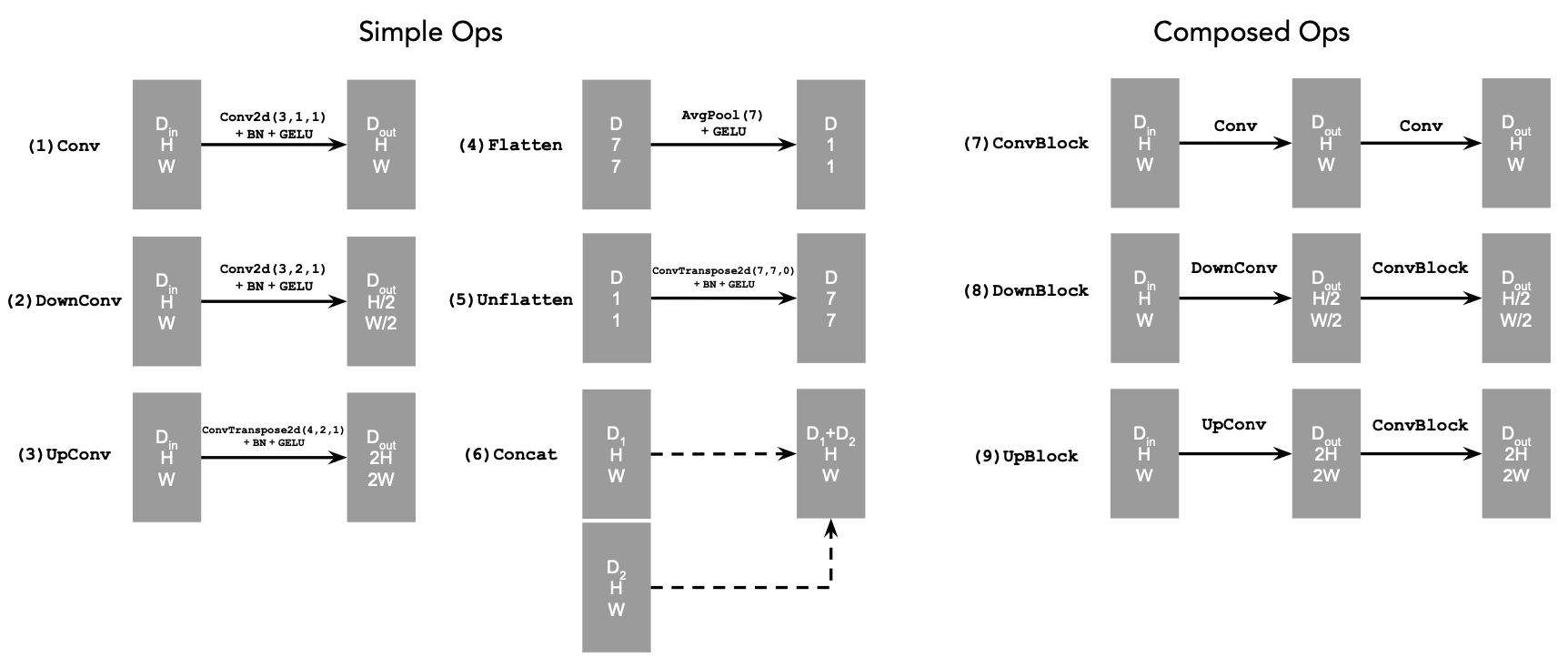
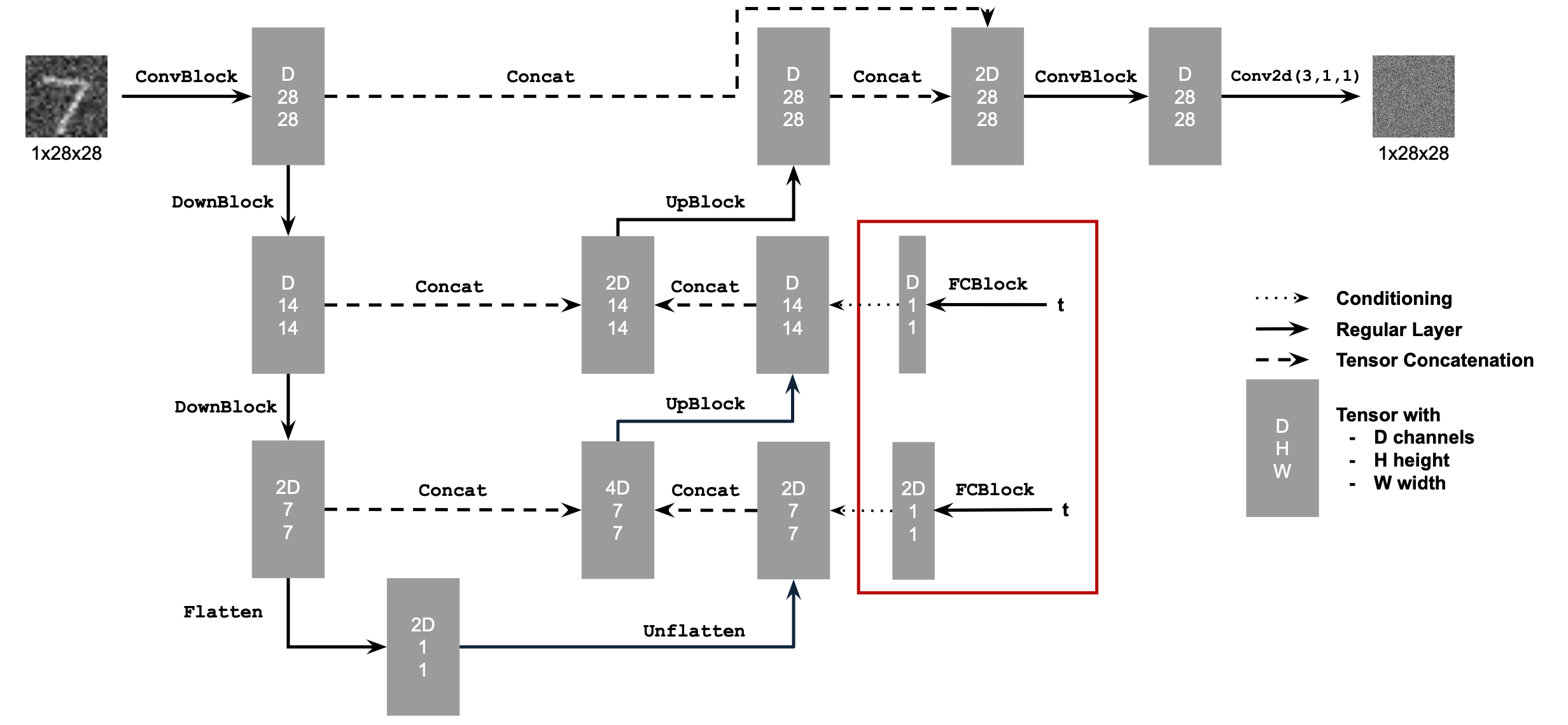
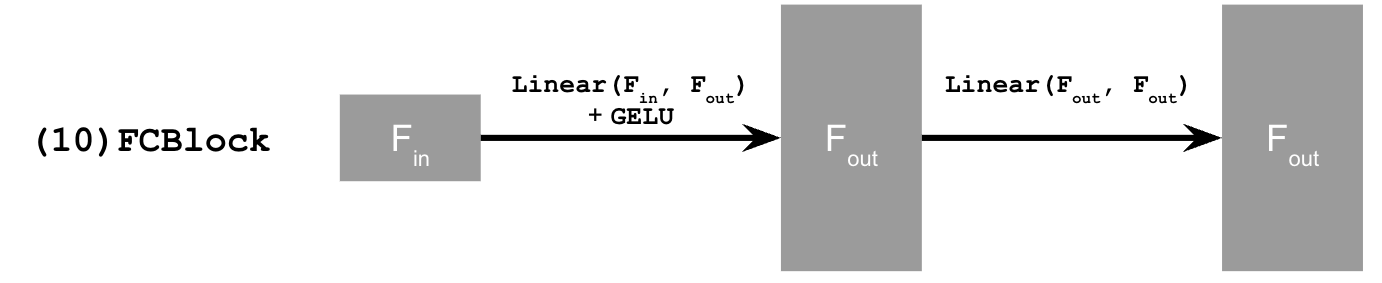
Project 5: Fun With Diffusion Models!

Austin Zhu

In this project, we explore the usage of diffusion models for the purposes of image generation and editing.

Part A: The Power of Diffusion Models!

As the first part of the project, we use the existing, pretrained DeepFloyd IF diffusion model and precomputed text embeddings to creating sampling loops and perform image editing tasks.

Part 1: Sampling Loops

The main idea between our diffusion models is to train a neural net that can iteratively reverse the noising process of an image. This way, we have a model that incremental takes a noisy image and moves it towards the desired image manifold, allowing us to generate new images.

1.1: Implementing the Forward Process

In order to do this, we first need to be able to add noise to images at our desired threshold. The equation that achieves this is: $$x_t = \sqrt{\bar{\alpha_t}}x_0 + \sqrt{1 - \bar{\alpha_t}}\epsilon$$ where \(\epsilon \sim N(0,1)\) is sampled at random. This is implemented in forward(im, t).

Our \(\bar{\alpha_t}\) variable is taken from the array alphas_cumprod, which gives us magnitudes for the desired noise at the different time periods. Below are the results of applying this forward method on an image of the Campanile for \(t \in [250, 500, 750]\):
Image of the Campanile.
Noised at t=250.
Noised at t=500.
Noised at t=750.

1.2: Classical Denoising

Before we use our pretrained neural nets to denoise the image, we first demonstrate the results of classical noising techniques via a low pass filter. Below are the results for the previously noised images:
Noised at t=250.
Noised at t=500.
Noised at t=750.
Gaussian blur denoise at t=250.
Gaussian blur denoise at t=500.
Gaussian blur denoise at t=750.
As we can see, this method isn't very effective especially at high noise levels. Note a kernel size of 15 and a \sigma of 2 were used in the gaussian blurs.

1.3: One-Step Denoising

Now we can actually try using our neural net to denoise the image. For now, we will try and estimate the original image in one step. Our neural net gives us a noise estimate \(\epsilon\) given the noised image and the timestep t, and we can then recover the estimated original image by solving for \(x_0\) in the original forward pass, giving: $$x_0 = \frac{x_t - \sqrt{1 - \bar{\alpha_t}}\epsilon}{\sqrt{\bar{\alpha_t}}}$$ Applying this formula, we get the following results:
Noised at t=250.
Noised at t=500.
Noised at t=750.
One-step denoise at t=250.
One-step denoise at t=500.
One-step denoise at t=750.
As we can see, this results are much better than those obtained using classical denoising in part 1.2.

1.4: Iterative Denoising

We can further improve this denoising process by iteratively denoising the image, instead of simply trying to do it in one pass. This can be thought of as each step taking a linear interpolated step for our current state towards the estimated clean image produced by 1.3. Additionally, instead of strictly iterating step by step down the values of t, we can take strided steps. For these examples, we will take strided steps of 30 from 990 to 0. The iterative step is defined below: $$x_{t'} = \frac{\sqrt{\bar{\alpha_{t'}}}\beta_t}{1 - \bar{\alpha_t}}x_0 + \frac{\sqrt{\alpha_t}(1-\bar{\alpha_{t'}})}{1-\bar{\alpha_t}}x_t + v_\sigma$$ where \(x_t\) is our current image, \(x_0\) is the estimate of the original image detailed in part 1.3, \(\bar{\alpha_t}\) is as defined before from alphas_cumprod, \(\alpha_t = \frac{\bar\alpha_t}{\bar\alpha_{t'}}\), \(\beta_t = 1 - \alpha_t\), and \(v_\sigma\) is a predicted noise that is also outputted by DeepFloyd.

Then, with t_start = 10, iterating following these steps along our strided_timesteps gives us the following results (with comparison to our methods provided):
Denoised at t=90.
Denoised at t=240.
Denoised at t=390.
Denoised at t=540.
Denoised at t=690.
Original.
Iteratively denoised.
One-step denoise.
Gaussian blurred denoise.

1.5: Diffusion Model Sampling

We can actually use our iterative_denoise function from part 1.4 to also generate new images. This is done by setting t_start = 0 and passing in random noise as our images. Five sampled images are shown below using this method:
5 sampled images using iterative denoising.

1.6: Classifer Free Guidance

The quality of the generated images in part 1.5 isn't the best, but we can improve this by implementing classifier free guidance, which uses a conditional and unconditional noise estimate (\(\epsilon_c\) and \(\epsilon_u\) respectively). Unconditional simply means that the prompt embeddings that we pass into the neural net, is that generated by the empty string ``''. Then, our noise estimate will be: $$\epsilon = \epsilon_u + \gamma(\epsilon_c - \epsilon_u)$$ where \(\gamma\) is a variable indicating the strength of the CFG. We can then use this noise estimate in our algorithm in 1.4 to iterative denoise the image as before. The results of sampling 5 images using this technique is shown below. Note how the image quality is much better.
5 sampled images using CFG iterative denoising.

1.7: Image-to-image Translation

We can use these methods to make edits to existing images by adding some noise to an image via forward(im, t), then running iterative_denoise_cfg starting from the same index you used to noise the image. This results in completely new images that resemble the original image. Results are shown on the following images, for noise levels [1, 3, 5, 7, 10, 20]:
Edited images
Original
Edited images
Original
Edited images
Original

1.7.1: Editing Hand-Drawn and Web Images

We can apply this to web images or our own hand-drawn images as well. Results are shown below:
Web edited images
Original
Hand-drawn edited images
Hand-drawn edited images

1.7.2: Inpainting

Using a binary mask \(\textbf{m}\) and slightly altering our denoising step, we can also force the model to only alter specific regions of the image. Our iterative step now has an additional: $$x_t \leftarrow \textbf{m}x_t + (1-\textbf{m})forward(x_{orig}, t)$$ which replaces everything outside of the mask with our original image with the proper amount of noise.

Results are shown below:
Inputs
Edited image
Inputs
Edited image
Inputs
Edited image

1.7.3: Text-Conditional Image-to-image Translation

Finally, we can alter our existing photos towards a desired output by altering the input of our text embedding. Results are shown below:
Edited towards rocketship
Original
Edited towards skull
Original
Edited towards snowy mountain village
Original

1.8: Visual Anagrams

Using these techniques, we can also generate visual anagrams, images that look like different subjects rightway up and upside down. This again requires us to make modifications to the noise estimate, shown below with prompt embeddings \(p_1\) and \(p_2\): $$\epsilon_1 = UNet(x_t, t, p_1)$$ $$\epsilon_2 = flip(UNet(flip(x_t), t, p_2))$$ $$\epsilon = (\epsilon_1 + \epsilon_2)/2$$ Note that \(\epsilon_2\) is generated from the flipped image on the second prompt embedding. Averaging these two noise estimates together gives a noise estimate that we can then apply the normal algorithm on.

Results for these hybrid images are shown below:
People around campfire + old man.
Amalfi cost + man wearing a hat.
Dog + waterfalls.

1.9: Hybrid Images

We can also use these methods to generate hybrid images similar to those in project 2. This will again involve altering our noise estimate as follows, for two prompt embeddings \(p_1\) and \(p_2\): $$\epsilon_1 = UNet(x_t, t, p_1)$$ $$\epsilon_2 = UNet(x_t, t, p_2)$$ $$\epsilon = f_{lowpass}(\epsilon_1) + f_{highpass}(\epsilon_2)$$ where we combine the two estimated by running a low pass filter on one, and a high pass filter on the other noise estimate. These filters are done by taking gaussian blurs and subtractions of those blurs, with kernel size 33 and \sigma 2.

Results are shown below:
Skull + waterfalls.
Pencil + dog.
Man + snowy mountain village.

Part B: Diffusion Models from Scratch!

Now we aim to train our own noise prediction models from scratch by building the neural net architecture.

Part 1: Training a Single-Step Denoising UNet

First, we will build a simple one-step denoiser. This UNet will take in some noisy image \(z\) and attempt to denoise it back to a clean image \(x\).

1.1: Implementing the UNet

Pictured below are diagrams of the UNet architecture and the operations contained within it.
UNet architecture.
Block operations
As we can see, this is a fairly standard UNet architecture with downsample, followed by upsampling, and plenty of cross feed-forward connections. Here, our UNet will take in \(1\times28\times28\) images and return \(1\times28\times28\) images, perfect for the MNIST dataset.

1.2: Using the UNet to Train a Denoiser

Next, we want to actually train our denoiser. Our inputs should be noised images and our outputs should be the clean versions of those images. We can generate these by taking our clean images form the MNIST dataset and adding noise to them, like in part A, to get our noisy images. $$z = x + \sigma\epsilon, \epsilon \sim N(0,I)$$ This noising process will look like the following:
Noised MNIST digits

1.2.1: Training

With these noised and clean image, we can start training our UNet. This is a fairly straightfoward neural net training process. We train on \(\sigma=0.5\), use L2 loss, have our UNet with hidden dimension 128, and use the Adam optimizer with a learning rate of 1e-4.

Loading in our MNIST training dataset with batch size 256 (shuffled beforehand), we train the UNet over 5 epochs and obtain the following training loss curve:
Below are sample results after the 1st and 5th epochs:
Sample results after epoch 1
Sample results after epoch 5

1.2.2: Out-of-Distribution Testing

We trained this denoiser on \(\sigma=0.5\). Now, we can test the denoiser's performance for different values of noise, \(\sigma = [0.0, 0.2, 0.4, 0.5, 0.6, 0.8, 1.0]\).
Sample 1
Sample 2

Part 2: Training a Diffusion Model

Now to implement diffusion, we will alter our UNet to predict noise instead of denoising the image, which is still an equivalent program. Now our loss function is: $$L = \mathbb{E}_{\epsilon,x_0,t}\|\epsilon_\theta(x_t, t)-\epsilon\|^2$$ as we would like to incorporate time-conditioning into our neural net as well.

2.1: Adding Time Conditioning to UNet

We can add time conditioning to the UNet by making the following changes to the architecture (adding FCBlocks):
Time Conditioned UNet architecture.
FCBlock
This conditioning operation of the FCBlock back into the UNet are implemented by just adding the output of the FCBlock to the intermediate value in question (either the unflatten or up1 outputs). Some work using einops.repeat does need to be done to cast the FCBlock output into the correct shape.

2.2: Training the UNet

Training time-conditioned UNet
Note, t should be normalized before being passed into the UNet. Now we can follow the above algorithm, with values of \(\bar{\alpha_t}\), \(\alpha_t\), and \(beta_t\) as specified in the spec or in the DDPM paper.

We follow this training algorithm with L2 Loss, hidden dimension 64, and an Adam optimizer with an initial learning rate of 1e-3, with an exponential decay scheduler with a gamma of \(0.1^{10/num_epochs}\). We again use the MNIST training dataset with batch size 128, being trained over 20 epochs. The resulting training loss curve is below:

2.3: Sampling from the UNet

Sampling from Time Conditioned UNet
Starting from total noise, we can use the above algorithm to obtain the following sampling results after epochs 5 and 20:
Sample results after epoch 5
Sample results after epoch 20

2.4: Adding Class-Conditioning to UNet

In order to add class conditioning, we need to one-hot encode our class vector \(c\) and then pass that into an FCBlock similar to the time-condition at the same locations. At those locations, the operation will now look like (for example, the unflatten):
unflatten = c1*unflatten + t1
where c1 and t1 are the outputs from the class and time conditioned FCBlock (with dimension adjusted according).

Additionally, during training, we have to implement dropout at a rate of \(p_{uncond}=0.1\), in which we set our one-hot vector to a vector of zeros in order to get enough training data for the unconditioned estimate needed for CFG.
Training Class Conditioned UNet
Following the above algorithm and using the same parameters, we get the following training loss curve:

2.5: Sampling from the Class-Conditioned UNet

Sampling from Class Conditioned UNet
Following the above algorithm, which implements CFG from part A, we get the following sampling results after epochs 5 and 20:
Sample results after epoch 5
Sample results after epoch 20