This project largely dealing with algorithms regarding facial morphing, computation of population
face means, and the caricatures we can create using them.
Part 1: Defining Correspondences
For the next three parts, I will focus on morphing my face and my friend Joe's face (also taking 180!).
The original images to morph as shown below.
 My picture.
My picture.
|
 Joe's picture.
Joe's picture.
|
In order to start the morphing process, we need to define the point correspondences between our two
faces, which I did using the provided labeling tool. These correspondences will allow us to clearly
define what sets of points should morph into each other to have a smooth transition. Then, I define
a consistent triangulation for both sets of points by averaging the points together, and finding a
triangulation using
scipy.spatial.Delaunay in order to get the Delaunay triangulation.
The results for both images are shown below:
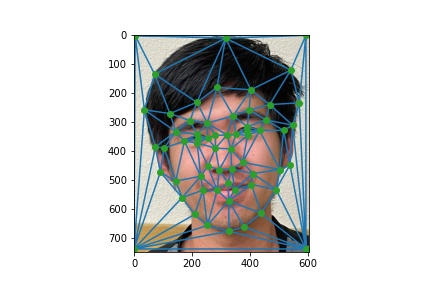 Triangulation on my image.
Triangulation on my image.
|
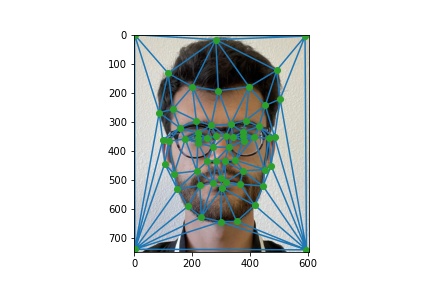 Triangulation on Joe's image.
Triangulation on Joe's image.
|



























